15 V(X ± Y) = V(X) V(Y) ± 2 COV(X,Y) = σ5X ± Y 16 If X and Y are independent, V(X ± Y) = V(X) V(Y) However, it is generally NOT TRUE that V(XY) = V(X)V(Y) Expectations Page 3 PROBLEMS HINT Keep in mind that µX and σX are constants 1 Prove that V(X) = E(X µX)5 = E(X5) µX5 HINT Rules 4, 5, and 8 are especially helpful here Solution Equation ExplanationStepbystep explanationWe need to expand (x− 32 y) 3 Suitable identities is (x−y) 3 =x 3 −3x 2 y3xy 2 −y 3 The value of (x− 32 y) 3 is= (x) 3 −3(x) 2 ( 3 manasvijaiswani86 manasvijaiswani86 Math Primary School Expand (xy^2)^3 please tell the answer 1 See answer manasvijaiswani86 is waiting for your help Add your answer and earn pointsExpand 1/12*((xyz)^6 2(x^6y^6z^6) 2(x^3y^3z^3)^2 4(x^2y^2z^2)^3 3(xyz)^2(x^2y^2z^2)^2) Natural Language;
How To Expand The Binomial X Y 10 Quora
(x y 2)^3 expand
(x y 2)^3 expand-All Math Calculators Polynomial calculators Expand and SimplifyKey Takeaways Key Points According to the theorem, it is possible to expand the power latex(x y)^n/latex into a sum involving terms of the form latexax^by^c/latex, where the exponents latexb/latex and latexc/latex are nonnegative integers with latexbc=n/latex, and the coefficient latexa/latex of each term is a specific positive integer depending on latexn/latex




X Y 2 Expand Aoierrico
The first one LATEX\sqrt{y^63 x^2 y^43 x^4 y^2x^6}/LATEX By the way, do you have any clue that how one can expand the expressions involving fractional exponents such as {x^2y^2}^(1/2) on the calculators such TI?Expand (x2)^3 (x 2)3 ( x 2) 3 Use the Binomial Theorem x3 3x2 ⋅23x⋅ 22 23 x 3 3 x 2 ⋅ 2 3 x ⋅ 2 2 2 3 Simplify each term Tap for more steps Multiply 2 2 by 3 3 x 3 6 x 2 3 x ⋅ 2 2 2 3 x 3 6 x 2 3 x ⋅ 2 2 2 3 Raise 2 2 to the power of 2 2This tells us that (x & y) is True whenever x and y are both True If an expression cannot be true, ie no values of its arguments can make the expression True, it will return False If an expression cannot be true, ie no values of its arguments can make the expression True, it will return False
A Resource for Free standing Mathematics Units Algebraic Expressions The Nuffield Foundation 2 Photocopiable Try these 1 Work out the value of these terms if x = 4, y = 5 and z = 2 a) 3y b) x2 c) x3 d) xy e) y3 f) 3z2 g) 2x y h) 4z – y i)This calculator can be used to expand and simplify any polynomial expression Site map;The second term of the sum is equal to Y The second factor of the product is equal to a sum consisting of 2 terms The first term of the sum is equal to X The second term of the sum is equal to negative Y open bracket X plus Y close bracket multiplied by open parenthesis X plus negative Y close parenthesis;
Since, x 3 3 x 2 y 3 x y 2 y 3 = (x y) 3 Let's factorize another polynomial This has both positive and negative terms, so it can be compared with the expansion of ( x − y ) 3In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveAn outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for their




How Do You Use The Binomial Series To Expand X Y 6 Socratic




Expand X X Y 3 3xy X Y
If we wanted to expand (x y) 52, (x y) 52, we might multiply (x y) (x y) by itself fiftytwo times This could take hours! Then we can expand (3xy)\times (3xy) using the FOIL method (the term FOIL stand for First, Outer, Inner, Last ) (3xy)\times (3xy)=3x3x3xyy3xyy Now we can further simply multiplying number with number and number is placed front of the each term (3xy)\times (3xy)=9{ x }^{ 2 }3xy3yx{ y }^{ 2 } The "xy" term and the "yxExpand (3 x 4 y) 2 Medium Open in App Solution Verified by Toppr (3 x 4 y) 2 is the product of two binomial expressons, which have the same terms (3 x 4 y) and (3 x 4 y) It can be expanded by the method of multiplying a binomial by a binomial On Comparing the identities with this product In this product a = 3 x and b = 4 y We can get the result of this product by




印刷可能 X Y 3 Expand X Y 1 3 Expand Pict4umioh




Expand 1x Y3 3 Maths Questions
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography,Click here👆to get an answer to your question ️ Expand ( 2x 5y 3z )^2 using suitable identities Join / Login >> Class 9 >> Maths >> Polynomials >> Algebraic Identities >> Expand ( 2x 5y 3z )^ Question Expand (− 2 x 5 y − 3 z) 2 using suitable identities Hard Open in App Solution Verified by Toppr (− 2 x 5 y − 3 z) 2 is of the form (a b c) 2 (a b c The final answer (ab)^5=a^55a^4b10a^3b^210a^2b^35a^1b^4b^5 The binomial theorem tells us that if we have a binomial (ab) raised to the n^(th) power the result will be (ab)^n=sum_(k=0)^nc_k^n *a^(nk)*b^(n) where " "c _k^n= (n!)/(k!(nk)!) and is read "n CHOOSE k equals n factorial divided by k factorial (nk) factorial" So
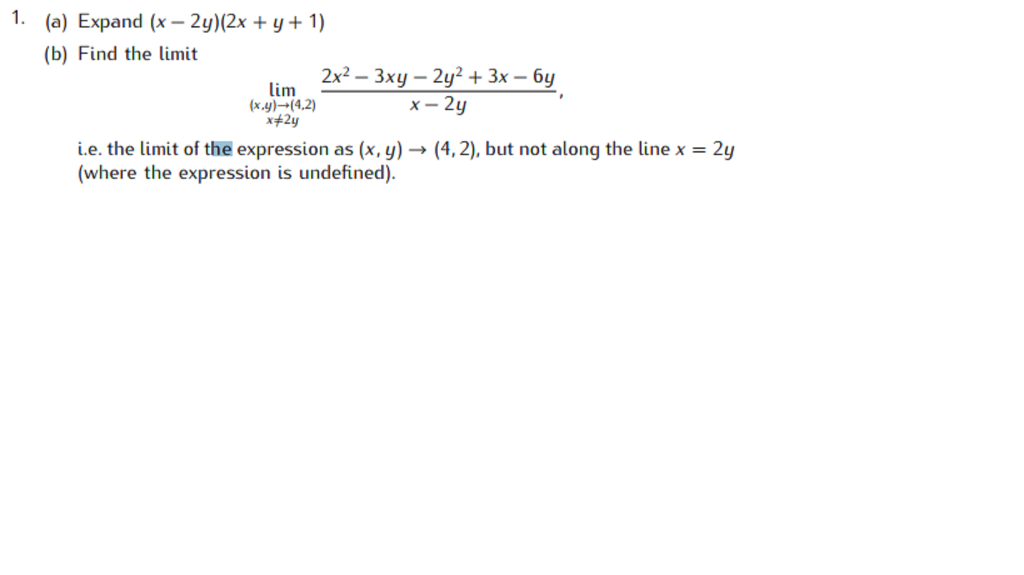



Solved 1 A Expand X 2y 2x Y 1 B Find The Limit Chegg Com




Solved 5 Expand The Following Expressions A X Y 2 Chegg Com
Expand ( X Y 2 )^3 Ask your question Secondary School Explanation (2x −y)6 The binomial theorem states that for any binomial (a b)n, the general expansion is given by (a b)n = twonCr ×an−r × br, where r is in ascending powers from 0 to n and n is in descending powers from n to 0 = two6C0(2x)6( −y)0 two6C1(2x)5( −y)1 two6C2(2x)4( −y)2 two6C3(2x)3( − y)3 two6C4(2x)2( −Expand(1 x y) (2 x)^3 Out16= 8 4 x 6 x^2 5 x^3 x^4 8 y 12 x y 6 x^2 y x^3 y ExpandAllSqrt(1 x)^2 Out17= Sqrt1 2 x x^2 ExpandSinx y, Trig > True Out18= Cosy Sinx Cosx Siny We expand the power expression \( (1x)^{10} \) into a regular polynomial using the following command Expand(1 x)^10 Out19= 11 10 x 45 x^2 1




ベスト X5 Y5 Expand シモネタ



How To Expand 2x Y 3 Quora
Using algebra to solve 4(x 3) 3(x 2)Firstly multiply through to get rid of brackets and add up the terms (xy2)^3 expandX^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \geProfessionals For math, science, nutrition, history 1 X Y 3 3 Expand Brainly In Using algebra to solve 4(x 3) 3(x 2)Firstly multiply through to get rid of brackets and add up the termsClick here 👆 to get an answer to your question ️ Expand (x2y3z)²There can be twoMath Calculators, Lessons and Formulas It is time to solve your math problem mathportalorg Math Tests;




X Y 2 3 Find The Expansion Of The Following Brainly In




How Can We Expand X Y 1 2 Youtube
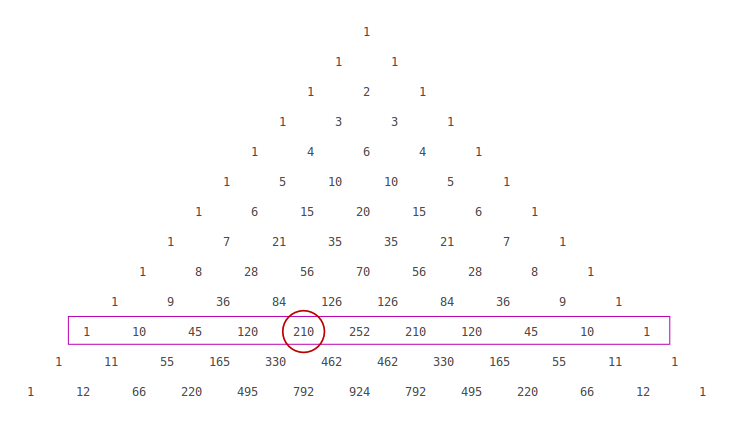
Simplify (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Rewrite using the commutative property of multiplication Multiply by Multiply by Multiply byExpand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions onlineIf we examine some simple binomial expansions, we can find patterns that will lead us to a shortcut for finding more complicated binomial expansions (x y) 2 = x 2 2 x y y 2 (x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 (x y) 4 = x 4 4 x 3 y 6 x 2 y 2 4 x




Expanding Logarithms




Lesson Worksheet Pascal S Triangle And The Binomial Theorem Nagwa
Take the square root of both sides of the equation x^ {2}y^ {2}3=0 Subtract 3 from both sides y^ {2}x^ {2}3=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0 Example 2 Important Deleted for CBSE Board 22 Exams Example 3 Important Deleted for CBSE Board 22 Exams Example 4 Deleted for CBSE Board 22 Exams Example 5 Important Deleted for CBSE Board 22 ExamsMy first and naive impression is that the result is 0 but according to Salinas, Introduction to Statistical Physics that's $3x^{1/2}y O(x/y)^3$ I think Taylor expansion would do it The thing




How Do You Expand X Y 6 Using Pascal S Triangle Socratic




無料でダウンロード X Y 2 3 Expand 6801 Expand The Binomial X 2 Y 2 3 Gambarsaekkg
How to expand two brackets algebra How to simplify (x3)(x4)We can use the distributive law for both x and 3 individually and multiply throughExpand lo g y 2 x 3 A 3 2 (lo g x lo g y) B 2 3 (lo g x lo g y) C 1 D 2 3 lo g x − lo g y Medium Open in App Solution Verified by Toppr Correct option is D 2 3 lo g x − lo g y Was this answer helpful?Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
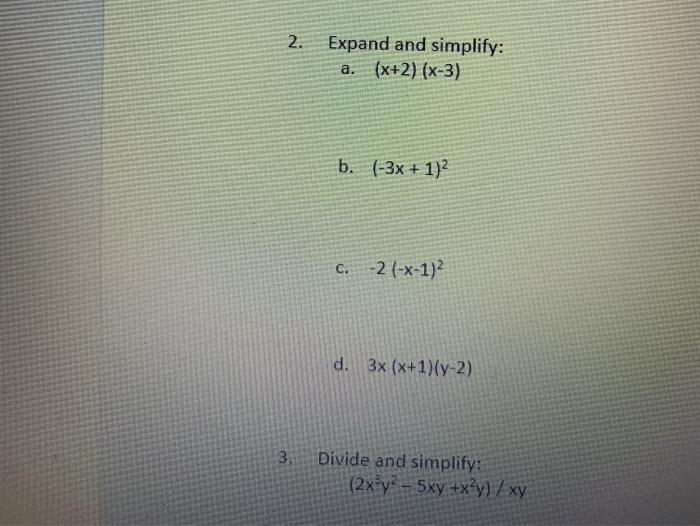



Solved 2 Expand And Simplify X 2 X 3 A B 3x 1 2 Chegg Com
Answer to Expand (2x y)^2 By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask your ownFree expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using thisContinue this process decrementing the power of x and incrementing the power of y until you place the term y n next to the final number 1x 5 5 x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 1y 5 Exercises Expand (2x y) 4 (x y) 6



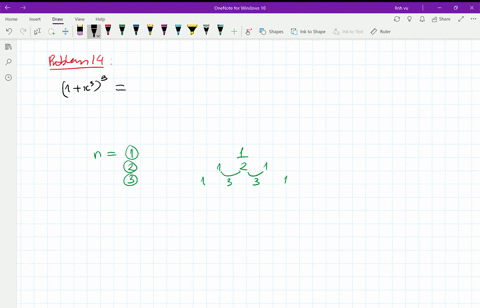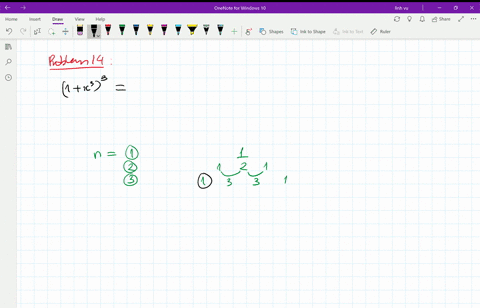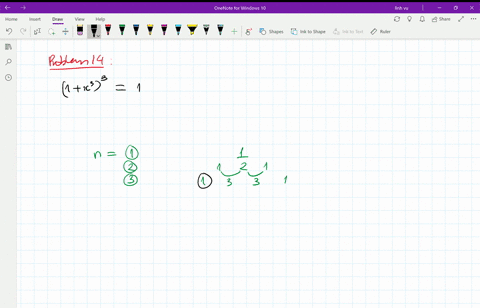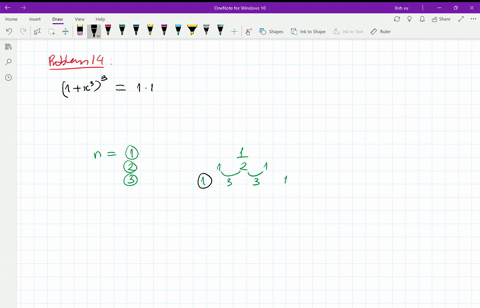
1



4 The Binomial Theorem
Click here👆to get an answer to your question ️ Expand (2x 3y)^2 Join / Login Question Expand (2 x 3 y) 2 Easy Open in App Solution Verified by Toppr (2 x 3 y) 2 = (2 x) 2 2 (2 x) (3 y) (3 y) 2 = 4 x 2 1 2 x y 9 y 2 Aliter (2 x 3 y) 2 = (2 x 3 y) (2 x 3 y) = 2 x (2 x 3 y) 3 y (2 x 3 y) = (2 x) (2 x) (2 x) (3 y) (3 y) (2 x) (3 y) (3 y) = 4 x 2 6 x yAnswer (1 of 4) " Let's solve the problem The expression is = (2x y)^3 The expression is equal to (2x y)^2 (2x y) Then it is equal to (4x^2 4xy y^2) (2x y) Then it is equal to 8x^3 4x^2y 8x^2y 4xy^2 2xy^2 y^3 Then it is equal to 8x^3 12x^2y 6xy^2 y^3, which is tExpand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3



How To Expand The Binomial X Y 10 Quora




X Y 2 Expand Aoierrico
Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graphSubtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 Reorder the terms Reorder the terms This is true for any x This is true for any x Use the distributive property to multiply xy by x^Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Expand And Simplify Binomial Squares 2x 3y 2 Youtube
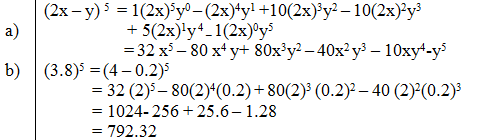



A Expand And Simplify The Binomial Expression 2x Y Sup 5 Sup B Use The First Four Terms Of The Expansion Above To Approximate The Value Of 3 8 Sup 5 Sup
Expand the following `(i) (3a2b)^(3) (ii) ((1)/(x)(y)/(3))^(3)` (iii) `(4(1)/(3x))^(2)`0 0 Similar questions Having given l o g 3 = 4 7 7 1 2 1 3, find the number of digits in (1) 3 4 3, (2) 3 2 7, and (3) 3 6 2, and the position of the first significantGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Using The Binomial Theorem College Algebra
Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2# Always expand each term in the bracket by all the other terms in the other brackets, but never multiply two or more terms in the same bracketThank you Best wishes PGInsert x n1 y next to the second number of Pascal's Triangle and add a "" sign 1x 5 5 x 4 y 10 10 5 1 ;
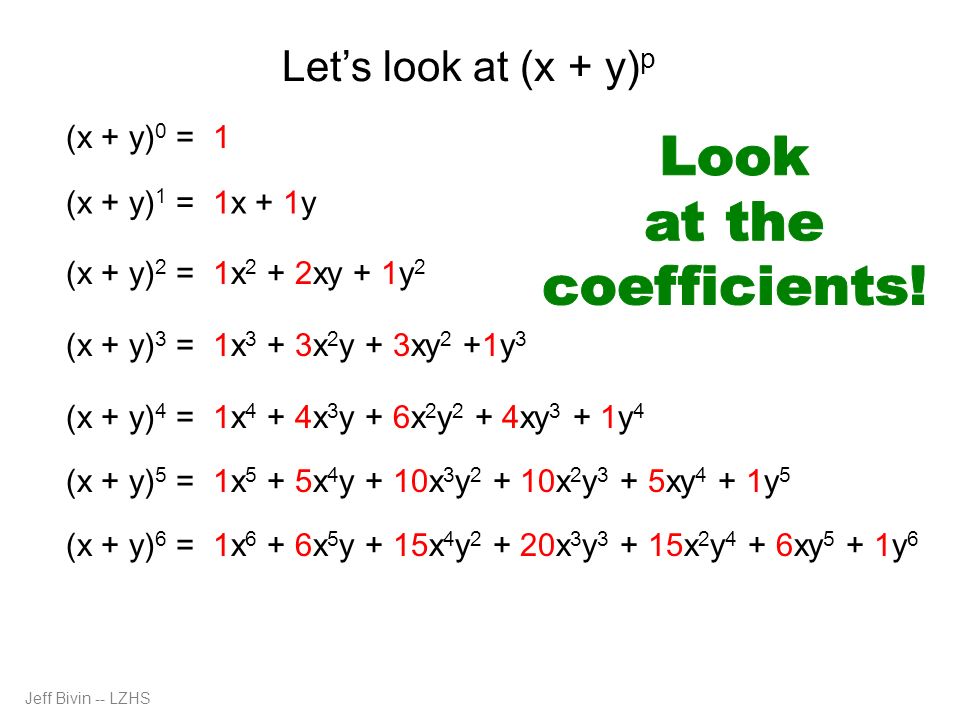



Binomial Expansion And More Ppt Download




Myriorama Cards Were Invented In France Around 13
Question Identify the binomial expansion of (xy)^3 Answer by rapaljer (4671) ( Show Source ) You can put this solution on YOUR website!So to find the expansion of (x − y) 3, we can replace y with (− y) in (x y) 3 = x 2 3 x 2 y 3 x y 2 y 3 This is the required expansion for ( x − y ) 3 Let's now use these identities toAlgebra Expand using the Binomial Theorem (xy)^3 (x − y)3 ( x y) 3 Because the binomial is raised to the 5th power, we need to use the 5th row of the triangle The 5th row is the one that features 1,5,10,10,5, and 1 In the expansion, x will be the first term and −y will be the second Thus, the expression looks like this For each term from Pascal's Triangle, the exponent of the first term, x, increases bySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Expand X Y 3 And X Y 2 Brainly In
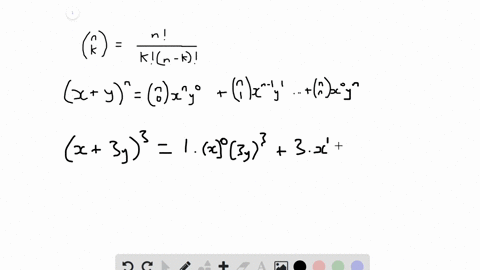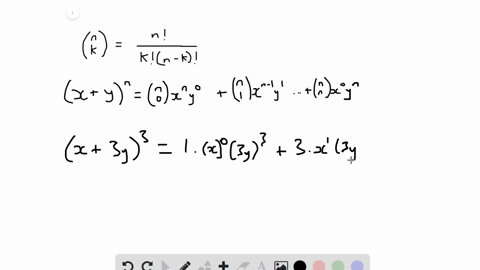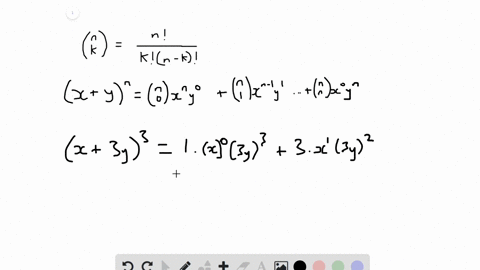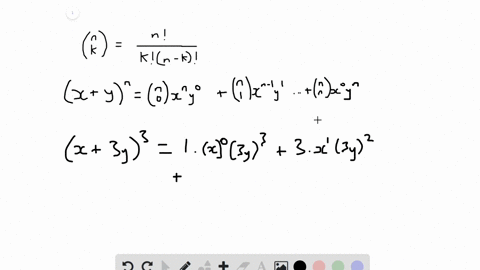



Solved In Exercises 9 30 Use The Binomial Theorem To Expand Each Binomial And Express The Result In Simplified Form X 3 Y 3




Binomial Theorem Wikipedia




Write Down The Expansion By The Binomial Theorem Of 3 X Y 2 To The Power Of Maths Binomial Theorem Meritnation Com




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Expand 1 X Y 3 3 Solve It Fastly Brainly In




Expand X 2 2y 5 Using Binomial Expansion Youtube



Mwn37wnp55mp M




Expanding Binomials Video Series Khan Academy




Myriorama Cards Were Invented In France Around 13




3 Expand With The Help Of Formula X Y 3 2



How To Expand X 2y 5 Using Binomial Expansion Quora




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube



What Is The Taylor Series Expansion Of Math E X Math About Zero Quora




Solved Use The Binomial Series To Expand The Function As A Chegg Com



If X Y 2 Then What Is The Value Of X Y 6xy Quora




Using The Binomial Theorem College Algebra




Binomial Theorem Protonstalk




Section 8 5 The Binomial Theorem Ppt Download



Solved Use Pascal S Triangle To Expand The Expression 2 X 3 Y 3




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
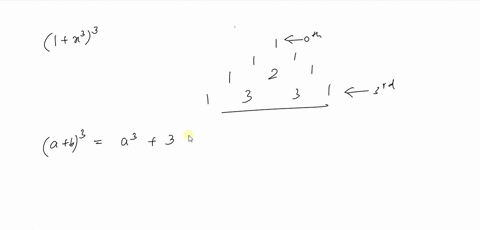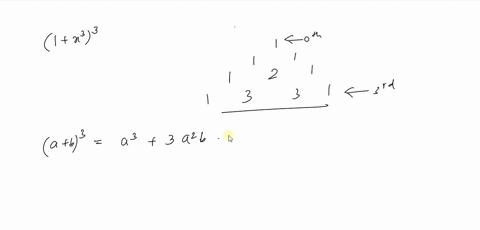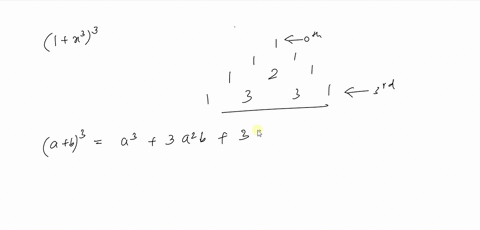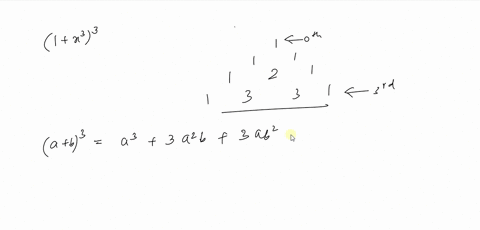



Solved Use Pascal S Triangle To Expand The Expression 2 X 3 Y 3
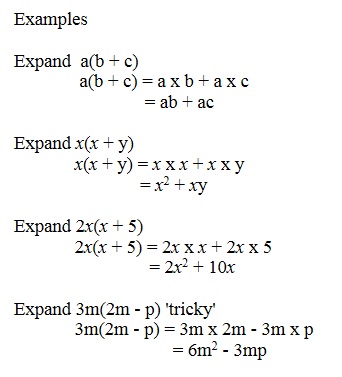



Algebra 5 Expanding Simplifying Mathtec




Solved Y 1 2x Y 0 Xy 2 X Y 0 A Solve The Chegg Com




9 5 The Binomial Theorem




Chapter 10 Further And Simplify 2 48 X Y Xy X Y 2 3 34 Acirc Circ




Sample Practice Exam 11 March Questions Transportation Studocu



1



Is There A Shortcut To Expand The Equation X Y Quora



Activity Z A Use The Laws Of Logarithms To Expand Gauthmath




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic




Obtainthe Taylor S Seriesexpansion Of X3 Y3 Xy 2 Interms Of Powers Of X 1 And Y 2 Up To Third Brainly In




How Do You Use Pascals Triangle To Expand 2y X 5 Socratic



22 X 1 3 Expand Pictures
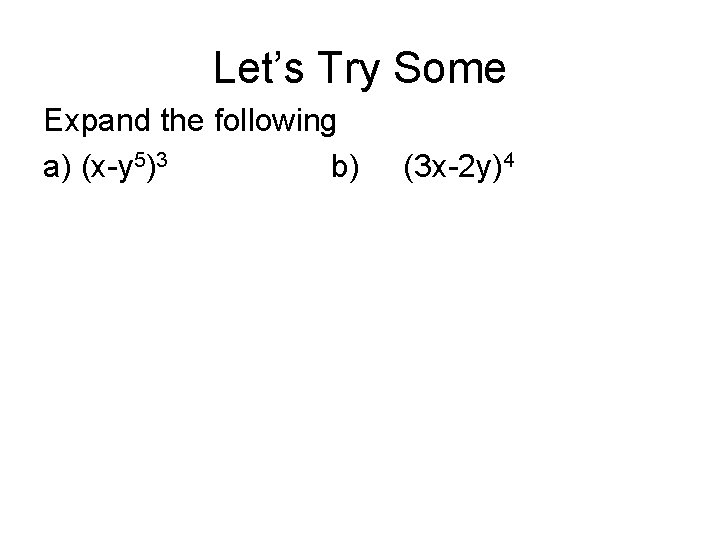



10 4 Pascals Triangle And The Binomial Theorem



Expand X Y 3 Sarthaks Econnect Largest Online Education Community




X Y 2 3 Find The Expansion Of The Following Brainly In




Assessment Algebra Dev Assessment In Algebra Lb 1 Hour 1 If A 2 B 3 And C 4 Evaluate Studocu



How Do You Find The Coefficient Of X 6 In The Expansion Of 2x 3 10 Socratic




Using Binomial Theorem Expand X Y 5 X Y 5 Dot And Hence




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Using Binomial Theorem Expand X Y 5 X Y And Hence Find The Value Of Root 2 1 5 Root 2 1 5 Maths Binomial Theorem Meritnation Com



Expand 2x Y3 X3 Square X2y Square Xy2 Squ Gauthmath




Binomial Expansion Binomial Expansions Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 The Binomial Theorem Provides A Useful Method Ppt Download



Using The Binomial Theorem College Algebra




How Do You Expand The Binomial X Y 5 Socratic



Expand 1 X Y 3 Whole Cube Studyrankersonline



Expand X Y Z Square Brainly In




Binomial Expansion Formulas Derivation Examples




Solved Exploit Symmetry To Expand The Product X 2 Y Y 2 Z Chegg Com




完了しました 1 X Y 2 Expand 1 X Y 2 Expand Blogjpmbahe5ydr



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Solved 1 6 Use The Binomial Expansion To Expand And Chegg Com
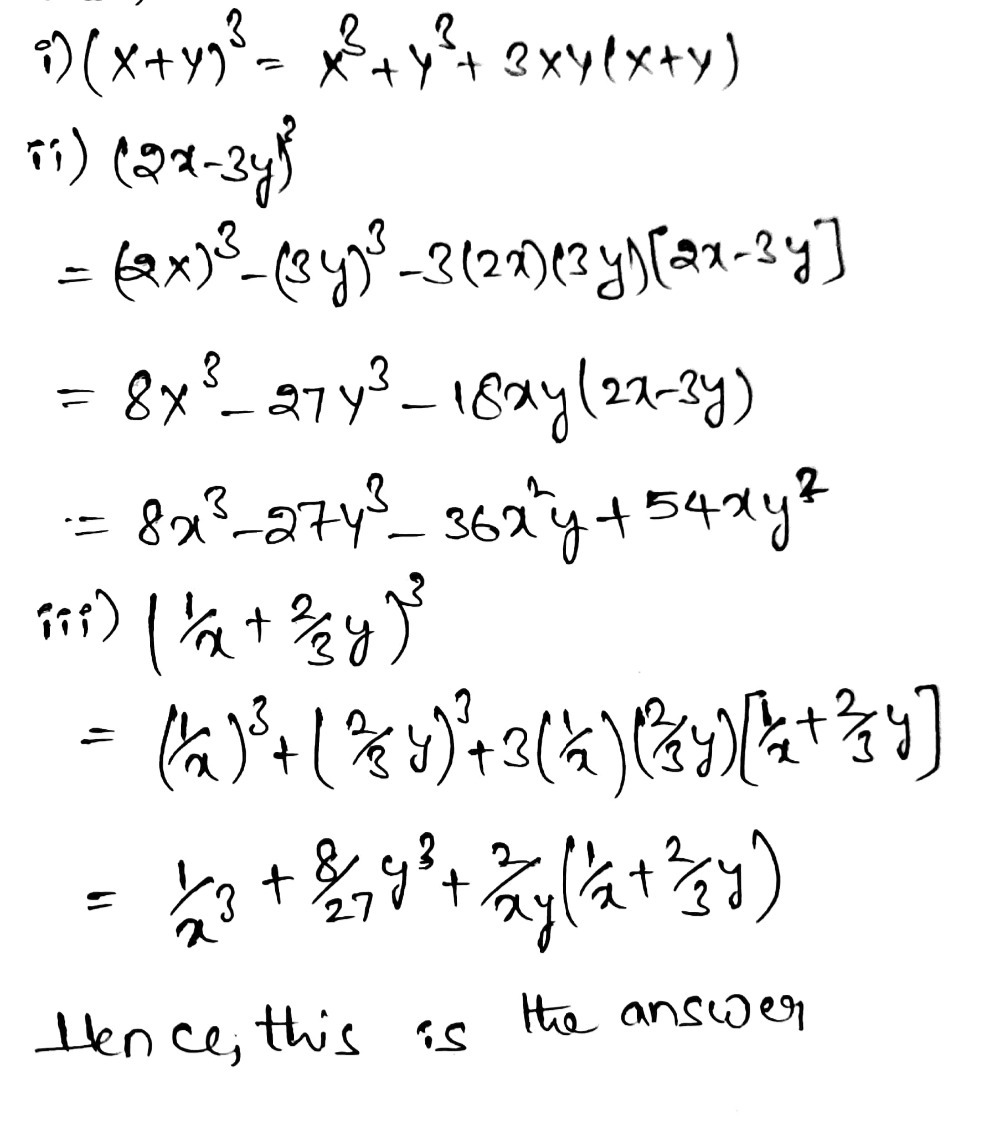



Expand With The Help Of Formulas X Y3 I Ii 2x 3y3 Gauthmath




Expand Log 3 Xy 2 Z 3




C4 Chapter 3 Binomial Expansion Exam Questions




Online Tutoring On Maths Binomial Theorem




Ppt Binomial Expansion And More Powerpoint Presentation Free Download Id




Binomial Expansion Made Easy Expand X Y Algebra Youtube



1




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf



1
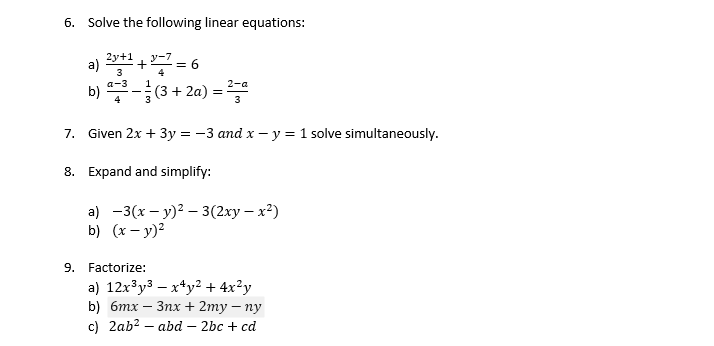



Solved 6 Solve The Following Linear Equations A 2y 1 3 Chegg Com




Conic Section From Expanded Equation Circle Parabola Video Khan Academy
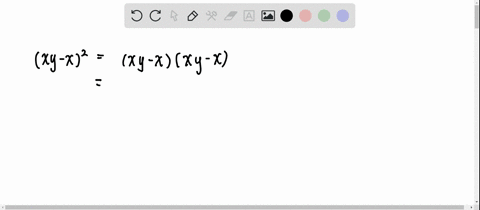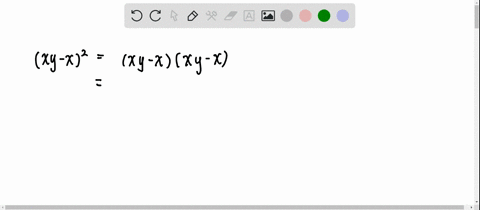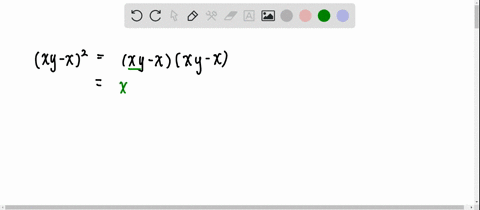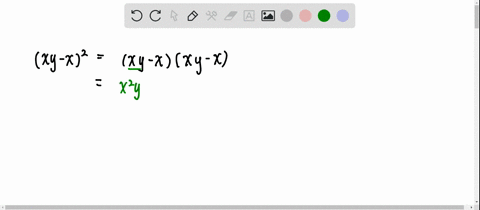



Solved Expand And Simplify Each Expression 3 X Y 2




Ex 2 5 6 Write The Following Cubes In Expanded Form I 2x 1 3




Simplify The Expression Ppt Video Online Download
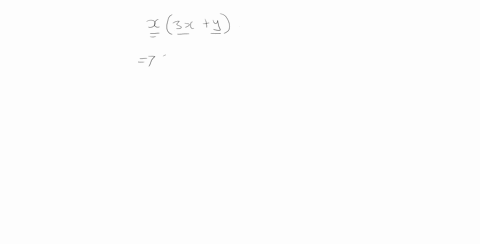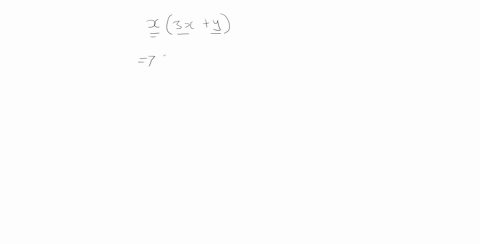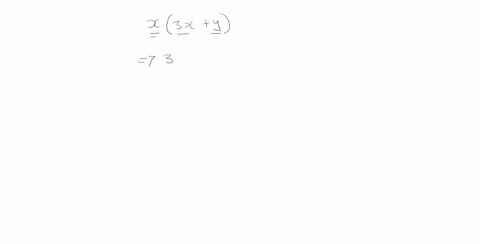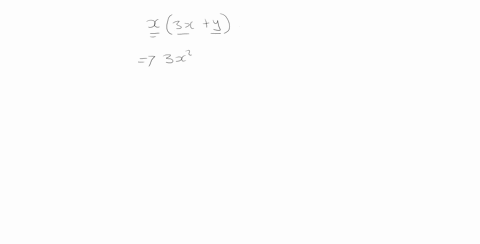



Solved Expand Each Expression 2 X Y Y



How To Expand X Y 7 Quora
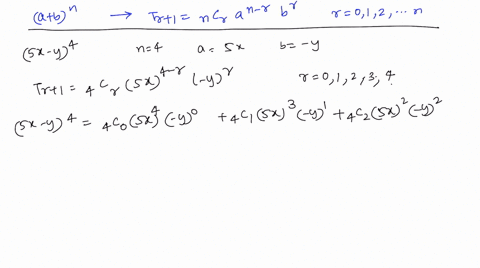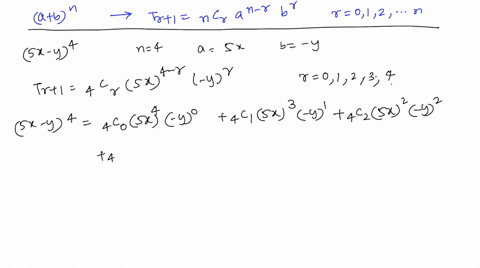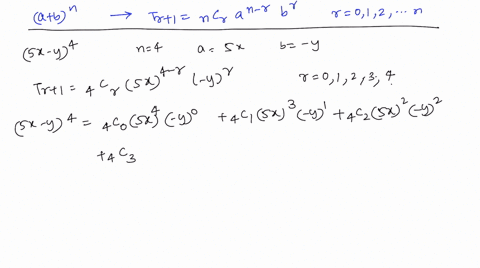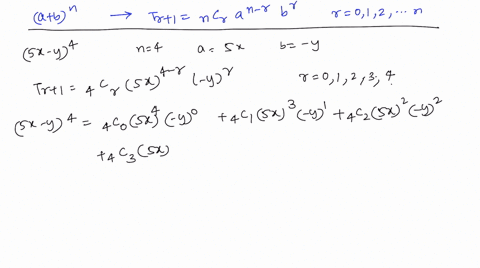



Solved Use The Binomial Theorem To Expand And Simplify The Expression 2 X Y 5



Expand 3x Y 5 Using The Binomial Theorem Mathsgee Q A Network




8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download




A Quick And Efficient Way To Expand Binomials Ppt Download



How Do You Use The Binomial Series To Expand 2x Y 9 Socratic




Taylor Series Expand X 2y 3y 2 In The Powers Of X 1 And Y 2 Up To 3 Degree Terms Youtube
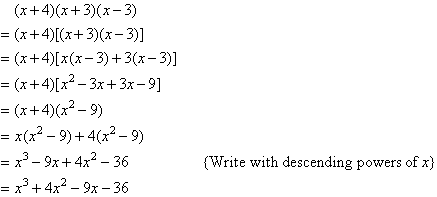



Expanding Three Terms




Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange



No comments:
Post a Comment